Entwicklung eines flexiblen eigenschaftsgeregelten Reckschmiedeprozesses
Geplant sind neue PDE-basierte Regelungskonzepte zur Stabilisierung optimaler Trajektorien. Dabei werden strukturmechanische Gleichungen linearisiert und in charakteristische Variablen transformiert. Dies ermöglicht eine Herleitung von Lyapunov-Funktionen, welche eine Schranke an Störungen darstellen. Die hergeleiteten algebraischen Feedback Regelungen sind unabhängig von der Diskretisierung. Existierende eindimensionale Resultate sollen auf mehrdimensionale Modelle erweitert werden und die Robustheit des Reglers bezüglich unsicherer Parameter soll untersucht werden.
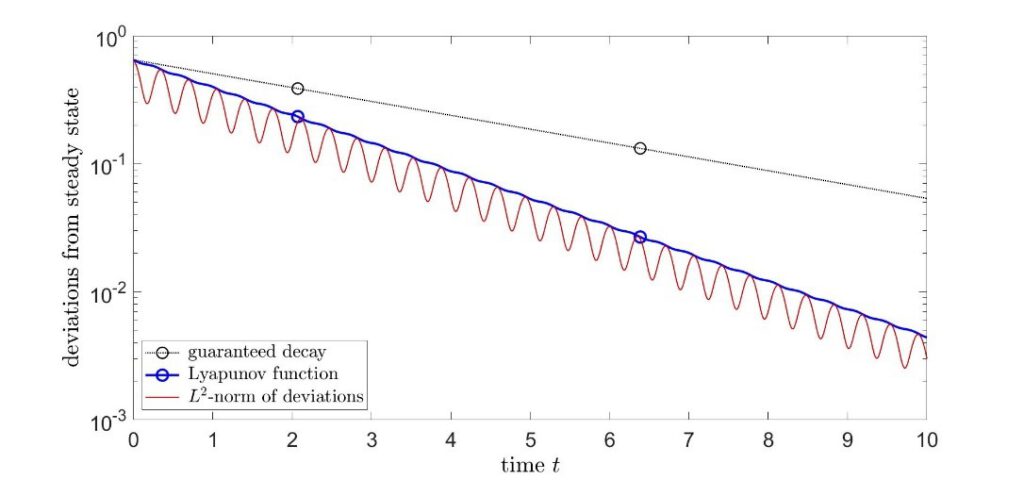
Ergebnisse der 1. und 2. Projektphase
In Phase eins konnte gezeigt werden, dass
(1) auf Basis von Lyapunovfunktionen aus dem umformtechnischen Anfangsrandwertproblem eine explizite Regelvorschrift hergeleitet werden kann, die ein exponentiell schnelles Abklingen von Störungen bewirkt,
(2) die entwickelte Regelvorschrift nicht von der gewählten Diskretisierung abhängt,
(3) die Herleitung der expliziten Regelvorschrift auf unsichere Zustände erweitert und ein beweisbar robuster und performanter Regler erhalten wird,
(4) ein hybrides Mikrostruktur- und Fließspannungsmodell bestehend aus einem physikalischen Modellrahmen und neuronalen Netzen prinzipiell in der Lage ist, die Mikrostrukturentwicklung im Werkstück zu beschreiben,
(5) das Modell mit Hilfe von Partikelfiltern online an neue Messdaten angepasst werden und so in die Zukunft extrapolieren kann (Beobachter),
(6) dass Softsensoren auf Basis von Werkstückregionen mit erfüllter Zielmikrostruktur mit Level-Set Methoden entworfen werden können (Ergebnis aus BA4253/12- 1) und
(7) der hergeleitete Regler gemeinsam mit dem Partikelfilter in einem einstufigen Flachstauchprozess im sowohl in der Simulation als auch im Experiment implementiert und validiert werden konnte.
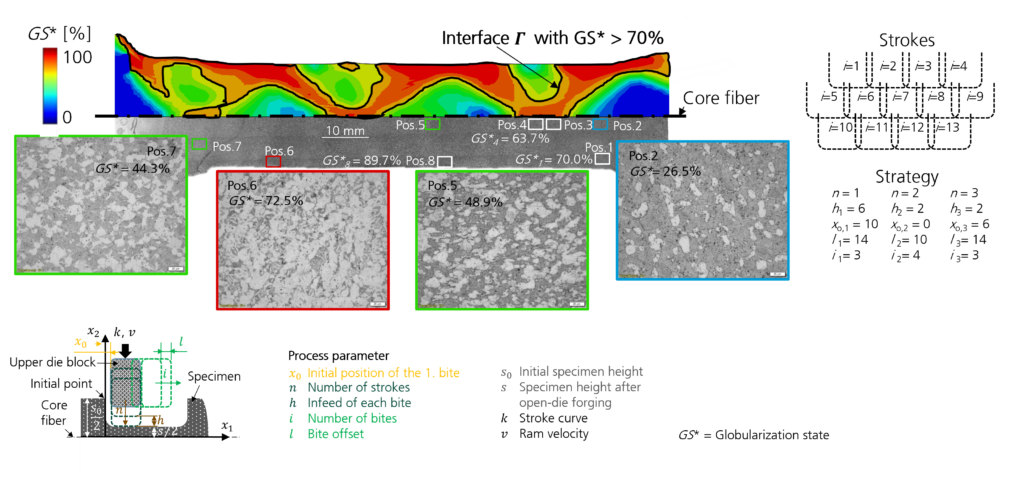
Somit wurde der Nachweis erbracht, dass die Globularisierung im Werkstück geschätzt und durch die Regelung auch bei Störungen die Zielwerte erreicht werden. Die Eigenschaftsregelung blieb bislang noch auf den Werkstückrand und somit auf homogen umgeformte Materialvolumina beschränkt.
Zusammenfassend wurden in Phase 2 die folgenden Ziele erreicht:
Es wurde (1) ein neuer experimenteller Aufbau realisiert, in welchem basierend auf Simulationen die Aktorik und Sensorik neu ausgelegt wurde. Durch getrennte Steuerung der Erwärmung und der Umformung wurden die Freiheitsgrade gegenüber des ursprünglich an der BTU Cottbus realisierten isothermen Versuchsstands signifikant erweitert. Weiter wurde die Sensorik so eingesetzt, dass mit der Steuerarchitektur eine Echtzeitregelung des Prozesses, basierend auf Messdaten, möglich ist.
Um eine automatisierte Echtzeitregelung zu gewährleisten, welche auch nachweislich auf Störungen reagiert, wurde (2) ein Softsensor auf Basis einer Level-Set Formulierung formuliert und analysiert. Dieser beschreibt die beobachtete Dynamik und ermöglicht eine mathematisch beweisbar stabile Regelung. Darüber hinaus konnte dieses Resultat (3) auf allgemeine Fälle und (4) stochastische Probleme erweitert werden.
Um den Input für den mathematischen Regler bereitzustellen, werden die gemessenen Größen durch einen Softsensor verarbeitet. Dieser extrapoliert Größen auf Basis der Messdaten und offline durchgeführten FE-Simulationen. Der Level-Set Softsensor wurde durch ein Neuronales Netz für Vorhersagen der Deformation und Globularisierung auf der gesamten Werkstückgeometrie ersetzt (5) ersetzt, welches Vorhersagen in 3D und Echtzeit ermöglicht.
Insgesamt haben die Ergebnisse der 2. Phase gezeigt, dass eine Regelung mittels der entwickelten Reglertheorie basierend auf der Level-Set Formulierung möglich ist. Allerdings sind die beobachteten Topologien der Gebiete mit erreichter Zielmikrostruktur beim Reckschmieden überwiegend nicht zusammenhängend. Zudem wurde gezeigt, dass bestimmte Zielzustände, z. B. eine Erreichung der Zielmikrostruktur auf einem zusammenhängen Kerngebiet des Werkstücks, mit den vorhandenen Freiheitsgraden nicht bei gleichzeitiger Erreichung der Zielgeometrie möglich ist.
Die verbleibenden Forschungsfragen sollen, auf Basis der in Phase 2 erzielten Ergebnissen, durch Erweiterung der Freiheitsgrade eine neuartige Kombination von Suchstrategien und Bayes‘scher Regelung und der 3D Echtzeitsimulationen des Ersatzmodells in Phase 3 gelöst werden.
Ziele der 3. Projektphase
Für das vorliegende Projekt wurden auf Basis der Ergebnisse der 1. und 2. Phase für die dritte Phase in Übereinstimmung mit den Zielsetzungen des SPP folgende Teilziele definiert:
- Untersuchung der benötigten Freiheitsgrade und Regelstrategien zur gemeinsamen Erreichung der gewünschten Zielgeometrie und des Zielgefüges
- Umsetzung der Eigenschaftsregelung inkl. Softsensor und Datenassimilation, sowie experimentelle Validierung für mehrhubige Reckschmiedeprozesse
- Mathematische Analyse des Ersatzmodells und des Reglers hins. Fehlerabschätzungen im Extrapolationsbereich und strukturenthaltene Eigenschaften des ML
- Quantitativer Nachweis der Eigenschaftsregelung für TiAl und Übertragung auf verallgemeinerte Reckschmiedeprozesse und einen weiteren Werkstoff
Kontakt
Fraunhofer-Institut für Gießerei-, Composite- und Verarbeitungstechnik IGCV
Projektleiter: Prof. Dr.-Ing. Markus Bambach
Projektbearbeiter: Dr.-Ing. Martin Feistle, Christian Linder
Institut für Geometrie und Praktische Mathematik der RWTH Aachen
Projektleiter: Prof. Dr. Michael Herty
Projektbearbeiter: Dr. Shaoshuai Chu, chu@igpm.rwth-aachen.de
Veröffentlichungen
- Bambach, M., Gerster, S., Herty, M. (2021) Online data assimilation of a hybrid flow stress model by particle filtering, CIRP Annals, https://doi.org/10.1016/j.cirp.2021.04.002
- Bambach, M., Imran, M., Sizova, I., Gerster, S., Herty, M. (2021) A soft sensor for property control in multi-stage hot forming based on a level set formulation of grain size evolution and machine learning, Advances in Industrial and Manufacturing Engineering, Volume 2, May 2021, 100041,https://doi.org/10.1016/j.aime.2021.100041
- Bambach, M., Gerster, S., Herty, M., Imram M. (2020) Feedback control for random linear hyperbolic balance laws, in revision for International Journal for Uncertainty Quantification, Int. Journal of Uncertainty Quantification, Volume 12, Issue 2, 2022, pp. 81-104, DOI: 10.1615/Int.J.UncertaintyQuantification.2021037183
- Bambach, M., Herty, M., Imran, M. (2021) Feedback stabilization of forming processes, Submitted to 6th IFAC Workshop on Mining, Mineral and Metal Processing, https://doi.org/10.1016/j.ifacol.2021.10.057
- Feistle, M.; Burger, S.; Li, R.; Bambach, M.; Thein, F.; Herty, M. (2022) New Machine Tool Control for Hot Forming of Lightweight Materials, 36. Aachener Stahlkolloquium – Umformtechnik “Ideen Form geben“,
Aachen, ISBN 978-3-95886-460-3. - Imran, M.; Bambach, M. (2018) Towards the damage evaluation using Gurson-Tvergaard-Needleman (GTN) model for hot forming processes, AIP Conference Proceedings, Volume 1960, Issue1, DOI: https://doi.org/10.1063/1.5035063.
- Imran, M.; Szyndler, J.; Afzal, M. J., Bambach, M. (2019) Dynamic recrystallization-dependent damage modeling during hot forming, International Journal of Damage Mechanics, Volume 29, Issue 2, DOI: https://doi.org/10.1177/1056789519848477.
- Imran, M.; Szyndler, J.; Afzal, M. J., Bambach, M. (2019) Towards the damage evolution for hot forming processes using Gurson-Tvergaard Needleman model – Coupled to dynamic recrystallization, AIP Conference Proceedings, Volume 2113, Issue 1, Volume 2113, Issue 1.
- Stendal, J.; Eisentraut, M.; Bambach, (2023) Developing an artificial neural network controller for accelerating the hot deformation of the titanium aluminide TNM-B1 using reinforcement learning and finite element simulations, Journal of Intelligent Manufacturing, https://doi.org/10.1007/s10845-023-02173-6
- Stebner, S. C.; Martschin, J.; Arian, B.; Dietrich, S.; Feistle, M.; Hütter, S.; Lafarge, R.; Laue, R.; Li, X.; Schulte, C.; Spies, D.; Thein, F.; Wendler, F.; Wrobel, M.; Vasquez, J. R.; Dölz, M.; Münstermann, S. (2023) Monitoring the evolution of dimensional accuracy and product properties in property-controlled forming processes, http://arxiv.org/abs/2305.19601.
- Herty, M.; Thein, F. (2022) Stabilization of a Multi-Dimensional System of Hyperbolic Balance Laws, Math. Control Relat. Fields (1. Revision eingereicht 06/2023), arxiv: https://arxiv.org/abs/2207.12006.
- Thein, F. (2023) Stabilization of a Multi-Dimensional System of Hyperbolic Balance Laws – A Case Study, Special Issue: 92nd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), Vol. 22(1), https://onlinelibrary.wiley.com/doi/abs/10.1002/pamm.202200056.
- Herty, M; Thein, F. (2023) Boundary Feedback Control for Hyperbolic Systems, ESAIM Optim. Control Calc. Var. (eingereicht), arxiv: https://arxiv.org/abs/2303.05598.
- Thein, F. (2023) The Shizuta – Kawashima Condition for the Barotropic SHTC Two Fluid Model, Proceedings of the XVIII International Conference on Hyperbolic Problems (HYP 2022) (accepted 06/2023).
- Petrik, J.; Ali, S. I.; Feistle, M.; Bambach, M. (2023) CrystalMind: A Surrogate Model for Predicting 3D Models with Recrystallization in Open-Die Hot Forging including an Optimization Framework. Mechanics of Materials 189(1), DOI: 10.1016/j.mechmat.2023.104875